Các dạng hệ phương trình và cách giải
Một số phương pháp giải phương trình và hệ phương trình là nội dung kiến thức mà các em đã được làm quen ở lớp 9 như phương pháp cộng đại số và phương pháp thế.
Bạn đang xem: Các dạng hệ phương trình và cách giải
Vậy sang lớp 10, việc giải phương trình và hệ phương trình có gì mới? các dạng bài tập giải phương trình và hệ phương trình có "nhiều và khó hơn" ở lớp 9 hay không? Chúng ta hãy cùng tìm hiểu qua bài viết dưới đây.
I. Lý thuyết về Phương trình và Hệ phương trình
1. Phương trình
a) Phương trình chưa biến x là một mệnh dề chứa biến có dạng: f(x) = g(x) (1).
- Điều kiện của phương trình là những điều kiện quy định của biến x sao cho các biể thức của (1) đều có nghĩa.
- x0 thỏa điều kiện của phương trình và làm cho (1) nghiệm đúng thì x0 là một nghiệm của phương trình.
Hay, x0 là nghiệm của (1) ⇒ f(x0) = g(xo).
- Giải một phương trình là tìm tập hợp S của tất cả các nghiệm của phương trình đó.
- S = Ø thì ta nói phương trình vô nghiệm.
b) Phương trình hệ quả
• Gọi S1 là tập nghiệm của phương trình (1)
S2 là tập nghiệp của phương trình (2)
- Phương trình (1) và (2) tương đương khi và chỉ khi: S1 = S2
- Phương trình (2) là phương trình hệ quả của phương trình (1) khi và chỉ khi S1 ⊂ S2
2. Phương trình bậc nhất
a) Giải và biện luận: ax + b = 0
° a ≠ 0: S = {-b/a}
° a = 0 và b ≠ 0: S = Ø
° a = 0 và b = 0: S = R
b) Giải và biện luận: ax + by = c
° a ≠ 0 và b ≠ 0: S = {x tùy ý; (c-ax)/b} hoặc S = {(c-by)/a; y tùy ý}
° a = 0 và b ≠ 0: S = {x tùy ý; c/b}
° a ≠ 0 và b = 0: S = {c/a; y tùy ý}
c) Giải và biện luận:
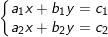
° Quy tắc CRAME, tính định thức:
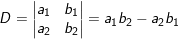
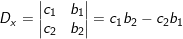
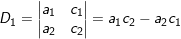
- Cách nhớ gợi ý: Anh Bạn (a1b2 - a2b1) _ Cầm Bát (c1b2 - c2b1) _ Ăn Cơm ((a1c2 - a2c1)
°
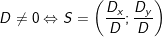
°
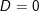
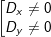
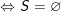
°
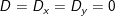
II. Các dạng bài tập toán về giải phương trình, hệ phương trình
° Dạng 1: Giải và biện luận phương trình ax + b = 0
* Phương pháp:
- Vận dụng lý thuyết tập nghiệm cho ở trên
♦ Ví dụ 1 (bài 2 trang 62 SGK Đại số 10): Giải và biện luận các phương trình sau theo tham số m
a) m(x - 2) = 3x + 1
b) m2x + 6 = 4x + 3m
c) (2m + 1)x - 2m = 3x - 2.
♠ Hướng dẫn:
a) m(x – 2) = 3x + 1
⇔ mx – 2m = 3x + 1
⇔ mx – 3x = 2m + 1
⇔ (m – 3)x = 2m + 1 (*)
+ Nếu m – 3 ≠ 0 ⇔ m ≠ 3, PT (*) có nghiệm duy nhất: x = (2m+1)/(m-3).
+ Nếu m – 3 = 0 ⇔ m = 3, PT (*) ⇔ 0x = 7. PT vô nghiệm.
- Kết luận:
m ≠ 3: S = {(2m+1)/(m-3)}
m = 3: S = Ø
b) m2x + 6 = 4x + 3m
⇔ m2x – 4x = 3m – 6
⇔ (m2 – 4)x = 3m – 6 (*)
+ Nếu m2 – 4 ≠ 0 ⇔ m ≠ ±2, PT (*) có nghiệm duy nhất:
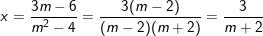
+ Nếu m2 – 4 = 0 ⇔ m = ±2
Với m = 2: PT (*) ⇔ 0x = 0, PT có vô số nghiệm
Với m =-2: PT (*) ⇔ 0x = -12, PT vô nghiệm
- Kết luận:
m ≠ ±2: S = {3/(m+2)}
m =-2: S = Ø
m = 2: S = R
c) (2m + 1)x – 2m = 3x – 2
⇔ (2m + 1)x – 3x = 2m – 2
⇔ (2m + 1 – 3)x = 2m – 2
⇔ (2m – 2)x = 2m – 2 (*)
+ Nếu 2m – 2 ≠ 0 ⇔ m ≠ 1, PT (*) có nghiệm duy nhất: x = 1
+ Xét 2m – 2 = 0 ⇔ m = 1, PT (*) ⇔ 0.x = 0, PT có vô số nghiệm.
Xem thêm: Diễn Viên Kim Hee Sun - Nhan Sắc Người Phụ Nữ Đẹp Nhất Hàn Quốc
- Kết luận:
m ≠ 1: S = {1}
m = 1: S = R
♦ Ví dụ 2: Biện luận số nghiệm của phương trình sau theo m: m2(x-1) = 2(mx-2) (1)
♠ Hướng dẫn:
- Ta có: (1) ⇔ m(m-2)x = (m-2)(m+2) (*)
◊ m ≠ 0 và m ≠ 2: (*) ⇔
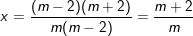
◊ m = 0: (*) ⇔ 0x=-4 (PT vô nghiệm)
◊ m = 2: (*) ⇔ 0x=0 (PT có vô số nghiệm, ∀x ∈ R)
- Kết luận:
m ≠ 0 và m ≠ 2: S = {(m+2)/m}
m = 0: S = Ø
m = 2: S = R
♦ Ví dụ 3: Giải và biện luận số nghiệm của phương trình sau theo m:
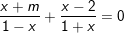
♠ Hướng dẫn:
- Ta có:
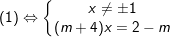
◊ m ≠ -4: (*) ⇔
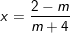
Điều kiện x ≠ ±1 ⇔
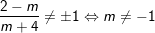
◊ m = -4: (*) ⇔ 0x = 6 (PT vô nghiệm)
- Kết luận:
m ≠ -4 và m ≠ -1: S = {(2-m)/(m+4)}
m = -4 hoặc m = -1: S = Ø
° Dạng 2: Xác định tham số để phương trình có nghiệm thỏa điều kiện
* Phương pháp:
- Vận dụng lý thuyết ở trên để giải
♦ Ví dụ 1 (bài 8 trang 63 SGK Đại số 10): Cho phương trình 3x2 - 2(m + 1)x + 3m - 5 = 0
Xác định m để phương trình có một nghiệm gấp ba nghiệm kia. Tính các nghiệm trong trường hợp đó.
♠ Hướng dẫn:
- Ta có: 3x2 – 2(m + 1)x + 3m – 5 = 0 (1)
(1) có hai nghiệm phân biệt khi Δ’ = b"2 - a.c > 0
⇔ (m + 1)2 – 3(3m – 5) > 0
⇔ m2 + 2m + 1 – 9m + 15 > 0
⇔ m2 – 7m + 16 > 0
⇔ (m – 7/2)2 + 15/4 > 0 , ∀m
⇒ PT (1) luôn có 2 nghiệm phân biệt, gọi x1,x2 là nghiệm của (1) khi đó theo Vi-et ta có:
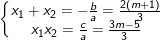
- Theo bài ra, phương trình có một nghiệm gấp ba nghiệm kia, giả sử x2 = 3x1, nên kết hợp với (I) ta có:
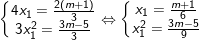
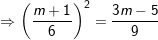
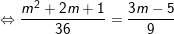
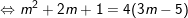
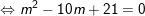
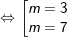
+ TH1 : Với m = 3, PT (1) trở thành: 3x2 – 8x + 4 = 0 có hai nghiệm x1 = 2/3 và x2 = 2 thỏa mãn điều kiện.
+ TH2 : m = 7, PT (1) trở thành 3x2 – 16x + 16 = 0 có hai nghiệm x1 = 4/3 và x2 = 4 thỏa mãn điều kiện.
- Kết luận: Để PT (1) có 2 nghiệm phân biệt mà nghiệm này gấp 3 lần nghiệm kia thì giá trị của m là: m = 3 hoặc m = 7.
♦ Ví dụ 2 : Tìm m để phương trình sau có nghiệm:
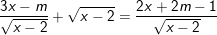
♠ Hướng dẫn:
- TXĐ: x>2
- Ta có: (1) ⇔ 3x - m + x - 2 = 2x + 2m - 1
⇔ 2x = 3m + 1 ⇔ x = (3m + 1)/2
- Kết hợp điều kiện (TXĐ): x>2, yêu cầu bài toán được thỏa mãn khi:
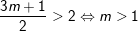
- Kết luận: Vậy khi m > 1, PT (1) có nghiệm x = (3m+1)/2.
° Dạng 3: Phương trình có chứa ẩn trong dấu giá trị tuyệt đối
* Phương pháp:
- Vận dụng tính chất:
1)
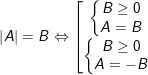
2)
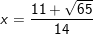
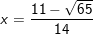
+ Với x 2 + 1 = -6x2 + 11x - 3
⇔ 5x2 -11x + 4 = 0
⇔
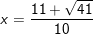
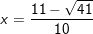
- Kết luận: PT đã cho có 2 nghiệm.
d) |2x + 5| = x2 + 5x + 1
+ Với x ≥ -5/2, ta có:
2x + 5 = x2 + 5x + 1
⇔ x2 + 3x - 4 = 0
⇔ x = 1 (thỏa) hoặc x = -4 (loại)
+ Với x 2 + 5x + 1
⇔ x2 + 7x + 6 = 0
⇔ x = -6 (thỏa) hoặc x = -1 (loại)
- Vật PT có 2 nghiệm là x = 1 và x = -6.
♦ Ví dụ 2: Giải và biện luận phương trình: |2x - m| = 2 - x (1)
♠ Hướng dẫn:
Ta có: (1)
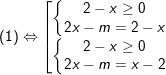
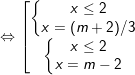
+)
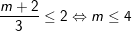
+)
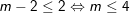
- Kết luận:
m ≤ 4. PT (1) có 2 nghiệm: x = (m+2)/3 hoặc x = m - 2.
m > 4: PT (1) vô nghiệm.
♦ Ví dụ 3: Giải và biện luận phương trình: |mx - 2| = |2x + m| (1)
♠ Hướng dẫn:
- Ta có:
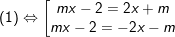
◊ Với PT: mx - 2 = 2x + m ⇔ (m - 2)x = m + 2 (2)
m ≠ 2: PT (*) có nghiệm x = (m+2)/(m-2)
m = 2: PT (*) trở thành: 0x = 4 (vô nghiệm)
◊ Với PT: mx - 2 = -2x - m ⇔ (m + 2)x = 2 - m (3)
m ≠ - 2: PT (*) có nghiệm x = (2 - m)/(2 + m)
m = -2: PT (*) trở thành: 0x = 4 (vô nghiệm)
- Ta thấy: m = 2 ⇒ x2 = 0; m = -2 ⇒ x1 = 0;
- Kết luận: m ≠ ±2: (1) có 2 nghiệm là:
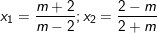
m = 2: (1) có nghiệm x = 0
m = -2: (1) có nghiệm x = 0
♥ Nhận xét: Đối vối giải PT không có tham số và bậc nhất, ta vận dụng tính chất 3 hoặc 5; Đối với PT có tham số ta nên vận dụng tính chất 1, 2 hoặc 4.
° Dạng 4: Hệ 2 phương trình bậc nhất 2 ẩn
* Phương pháp:
- Ngoài PP cộng đại số hay PP thế có thể Dùng phương pháp CRAME (đặc biệt phù hợp cho giải biện luận hệ PT)
♦ Ví dụ 1 (bài 2 trang 68 SGK Đại số 10): Giải hệ PT
a)
b)
♠ Hướng dẫn:
- Bài này chúng ta hoàn toàn có thể sử dụng phương pháp cộng đại số hoặc phương pháp thế, tuy nhiên ở đây chúng ta sẽ vận dụng phương pháp định thức (CRAME).









