Lục giác, lục giác đều
Hình lục giác là một hình học đặc biệt trong cấu trúc hình học, được coi làhình có diện tích các cạnh nhỏ nhất nhưng lại phủ chứa được lượng không gian lớn nhất và hình lục giáclà hình đượcứngdụng khá rộng rãi trong tính toán thực tế. Chúng ta sẽ tìm hiểu công thức tính toán này trong bài viết ngay dưới đây của chúng tôi nhé !
I. Định nghĩa
Một hìnhlục giáchoặchình sáu cạnhlà mộtđa giác, một hình thể tronghình học phẳng, bao gồm sáu góc và sáu cạnh.
Bạn đang xem: Lục giác, lục giác đều
Diện tích lục giác thường:Muốn tính diện tích của hình lục giác thường, ta có thể chia hình lục giác thành 4 hình tam giác, tính tổng diện tích của các tam giác đó là tìm ra diện tích của hình lục giác.
Công thức tính chu vi lục giác: P = 6.aVới: P là chu vi và a là cạnh của lục giác
II. Lục giác đều
1. Khái niệm
Nếu sáu cạnh có chiều dài bằng nhau, nó được gọi là một hình lục giác sáu cạnh đều. Chỉ khi tất cả các góc có cùng kích thước, và các cạnh bằng nhau, mới gọi làlục giác đều. Một hình khối với hai đáy hình lục giác gọi làlục lăng.
2. Đặc điểm hình lục giác đều
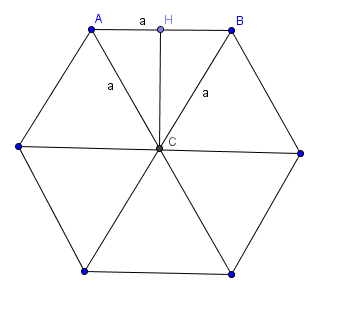
Các cạnh bằng nhau và các góc ở đỉnh bằng nhau. Tâm của đường tròn ngoại (và nội) tiếp là tâm đối xứng quay (tỏa tròn). Tổng số đo các góc ở đỉnh là: \((n.180^{\circ} -360^{\circ})=180^{\circ}.(n-2)\) ,mà n là số cạnh của đa giác đều. Vậy độ lớn của góc ở đỉnh là: \(180^{\circ}.\dfrac{n-2}{n}\). Gọi R và r là bán kính của đường tròn ngoại và nội tiếp của đa giác đều, gọi cạnh của đa giác đều là a , thì ta có: \(a=2.R.sin(\dfrac{360^{\circ}}{2}.n)=2.r.tan(\dfrac{360^{\circ}}{2}.n) \) Các cạnh của nó dài đúng bằng bán kính đường tròn ngoại tiếp. Nếu nối tâm đường tròn ngoại (và nội) tiếp với các đỉnh của lục giác thì ta sẽ có 6 tam giác đều.3. Cách vẽ lục giác đều
Có nhiều cách vẽ hình lục giác đều mà bạn có thể tham khảo sau đây:
Cách 1:Ta vẽ đường tròn,trong hình tròn vẽ đường kính lấy 2 điểm của đường kính nằm trên đường tròn vẽ 2 cung có bán kính bằng bán kính hình tròn lúc đầucác điểm giao nhau của các hình tròn và hai đầu của đường kính là 6 điểm của hình lục giác đều.
Cách 2:Bạn có thể vẽ lục giác đều với độ dài cạnh cho trước như sau: Lấy số đo độ dài của cạnh lục giác đều làm bán kính để vẽ 1 đường tròn sau đó đặt liên tiếp các dây cung dài bằng bán kính đó lên đường tròn vừa vẽ được (Đặt được 6 dây cung bằng nhau liên tiếp), các mút chung của 2 dây liên tiếp lần lượt chính là các đỉnh của lục giác đều có độ dài cạnh cho trước.
Cách 3: Bạn hãy vẽ ra 1 tam giác đều rồi sau đóvẽ cho nó 1 đường tròn ngoại tiếptừ 1 đỉnh của tam giác kéo dài qua tâm đường tròn cắt đường tròn tại 1 điểm nữa (điểm A). Từ điểm A này vẽ 1 tam giác đều có đường cao là đường kéo dài qua tâm hồi nãy.
Cách 4:Bạn vẽ 1 đường tròn (C) bán kính bất kì, đặt tâm compa nằm trên đường tròn (C), quay các dg tròn đồng tâm với (C) cắt (C) tại các điểm là đỉnh lục giác cần tìm. Tâm của đườngtròn sau là giao điểm của đườngtròn trước với (C).
Tìm hiểu thêm:Bảng công thức logarit đầy đủ từ A đến Z để giải bài tập
4. Diện tích lục giác đều
Để tính được diện tích của hình lục giác đều, ta sử dụng công thức như sau:
\(S = \dfrac{3\sqrt3 a^2}{ 2}\)
Trong đó:
S là kí hiệu diện tích a là độ dài cạnh của lục giácMới nhất:Công thức tính diện tích hình lục giác
III. Bài tập luyện tập về lục giác
Bài 1: Cho lục giác lồi ABCDEF biết rằng mỗi đường chéo AD,BE,CF chia nó thành 2 phần có diện tích bằng nhau.Gọi M,N lần lượt là giao của EB với AC và FD, P và Q lần lượt là giao của AD với BF và CE.CMR:
a) PM song song với NQ.
b) AD,BE,CF đồng quy.
Bài 2: CMR nếu ngũ giác có các góc bằng nhau và nội tiếp 1 đường tròn thì ngũ giác ấy đều.
Bài 3: Các cạnh đối diện AB và DE,BC và EF,CD và FA của lục giác ABCDEF song sog.CMR diện tích tam giác ACE=diện tích tam giác BDF.
Bài 4: Cho lục giác ABCDEF có các cạnh đối song song.
a) CMR diện tích tam giác ACE lớn hơn hoặc bằng 1 nửa diện tích ABCDEF.
b) CMR nếu lúc giác có các góc bằng nhau thì hiệu các cạnh đối diện bằng nhau.
Bài 5: Cho ngũ giác lồi ABCDE có tam giác ABC và CED đều.Gọi O là tâm của tam giác ABC.M và N lần lượt là trung điểm của BD và AE.CMR tam giác OME và tam giác OND đồng dạng.
Bài tập về lục giác đều có lời giải:
IV. Ứng dụng hình lục giác trong cuộc sống
1. Các lỗ tổ ong mật có hình lục giác đều
Như các bạn đã biết, loài ong được coi là những kiến trúc sư đại tài trong thế giới loài vật. Khi quan sát tổ ong,bạn sẽ nhận thấy các lỗ trên tổ đều là những hình lục giác đều có sáu góc, sáu cạnh bằng nhau nằm sát kề nhau, sở dĩ con ong lựa chọn cách xây tổ như vậy vì chu vi lục giác nhỏ nhất trong số các hình tam giác hay hình vuông; hơn nữa cấu trúc lỗ tổ hình lục giác có sức chứa tối đa và có độ bền lớn so với các loại hình học khác.Lục giác đều là một hình mà khi con ong xây tổ thì nó sẽ lấy hình này làm "tế bào" và nhờ đó nó sẽ cần dùng ít nguyên vật liệu xây dựng nhất, để đạt được "không gian sống" cho các ong con hiệu quả nhất.
2. Nước Pháp là "đất nước hình lục giác"
Chắc hẳn khi nhắc đến nước Pháp (Cộng hòa Pháp), bạn sẽ nghĩ ngay đến tháp Ép-phen, một kiệt tác nổi tiếng và những cánh đồng hoa oải hương tím ngắt,... nhưng bạn cũng sẽ rất bất ngờ khi biết phạm vi lãnh thổ nước Pháp trên bản đồ có hình lục giác sáu cạnh rất thú vị. Bởi vậy mà nước Pháp còn được gọi là "đất nước hình lục lăng".
3. Hình lục giác là hình khối phổ biến trong xây dựng lăng mộ
Chắc hẳn đã có đôi lần bạn nhìn thấy những ngôi mộ bằng đá được xây dựng theo hình lục giác đều, bạn có cảm thấy tò mò về nó không, vậy tại sao khối hình này lại được chọn lựa để xây dựng lăng mộ? Lí do đó chính làkhối lục giác được chọn là bởi khối hình này có ý nghĩa rất lớn trong tự nhiên, nó biểu tượng cho sự hoàn hảo và đẹp đẽ của tự nhiên. Hơn thế nữa, cách xây dựng theo hình lục giác sẽ giúp tiết kiệm được vật liệu mà công trình vẫn có thể giữ được độ bền chắc, bên cạnh đó vẫn giữ được ý nghĩa về phong thủy.
4.Một ốc vít với hình lục giác bên trong
Việc nắm được công thức về lục giáclà rất cần thiết và quan trọng trong quá trình giải các bài tập hình học, bởi vậy chúng tôi hi vọng với những kiến thức chia sẻ trên đây sẽ hữu ích đối với độc giả, đặc biệt là các em học sinh trong quá trình làm bài tập ở nhà cũng như khi học trên lớp. Nếu các em sưu tầm được công thức hay cách giải nào thú vị, các em có thể chia sẻ cùng chúng tôi để kiến thức Toán học trở nên phong phú hơn!









